Jedes Jahr findet in der Woche vor den Semesterferien die Projektwoche Angewandte Mathematik statt. Diese Veranstaltung bietet mathematisch begabten Schülern und Schülerinnen unterschiedliche Möglichkeiten sich intensiv mit mathematischen Fragestellungen zu beschäftigen. Maximilian Donnermair und Lukas Aichhorn aus der 7C nahmen dieses Jahr an dieser Projektwoche teil und verfassten einen Erfahrungsbericht.
Ein Erlebnisbericht von Maximilian Donnermair und Lukas Aichhorn (7C)
Im Normalfall hat es sich in der letzten Schulwoche vor den Semesterferien ausgetestet. Aus diesem Grund wird die Projektwoche „Angewandte Mathematik“ jedes Jahr in dieser Woche veranstaltet. Es ist eine Gelegenheit für junge Mathematikinteressierte von der 9. bis zur 13. Schulstufe, ihre Talente zu fördern und tiefer in das Gebiet der Zahlen einzutauchen. Während andere Schüler versuchen, Mathematik aus den meisten anderen Bereichen ihres Lebens fernzuhalten, wird den Teilnehmern hier ihr Zusammenhang zu Fachbereichen wie der Biochemie, Bildbearbeitung, Architektur und vielen weiteren beigebracht. Im Folgenden werden die zwei Kurse, die von zwei Schülern des BORG besucht wurden, vorgestellt:
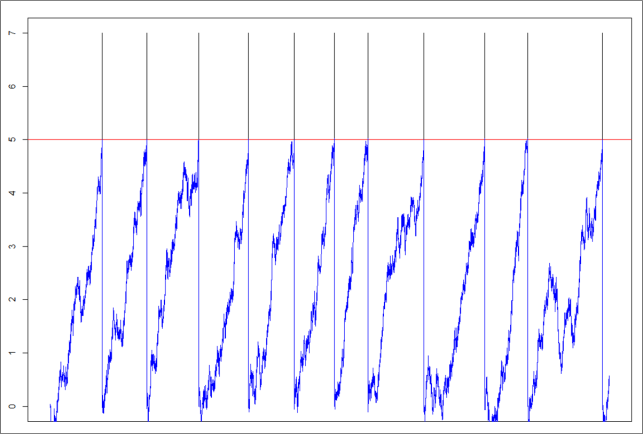
In „Der Zufall im Gehirn“ ging es darum, die Potenziale von Neuronen mathematisch mithilfe von Wahrscheinlichkeitsfunktionen darzustellen. Zu Anfang des Kurses arbeiteten wir verschiedene Modelle aus, mit einer Zufallsvariable Vorgänge zu modellieren. Wir leiteten alle möglichen Formeln her und lernten die Anwendungsbereiche verschiedener Zufallsverteilungen. Nun kann man sagen, eine Nervenzelle depolarisiert nicht zufällig. Doch was ist schon zufällig? Nach einer stundenlangen Diskussion während und nach dem Mittagessen an einem Tag – Was gäbe es sonst zu Tisch zu besprechen? – kamen wir bei dieser philosophischen Frage auch auf keinen grünen Zweig. Wir nahmen es hin und konnten schließlich eine Funktion in die Programmiersprache „R“ implementieren, die das Membranpotenzial einer Nervenzelle approximieren soll. Wir gaben verschiedene Werte in die Variablen der Funktion ein und bekamen so ein einigermaßen anschauliches Bild für das Integrate&Fire-Modell, das ein Neuron darstellt, dessen elektrische Spannung immer positiver wird, bis es schließlich einen „Spike“ abschießt.
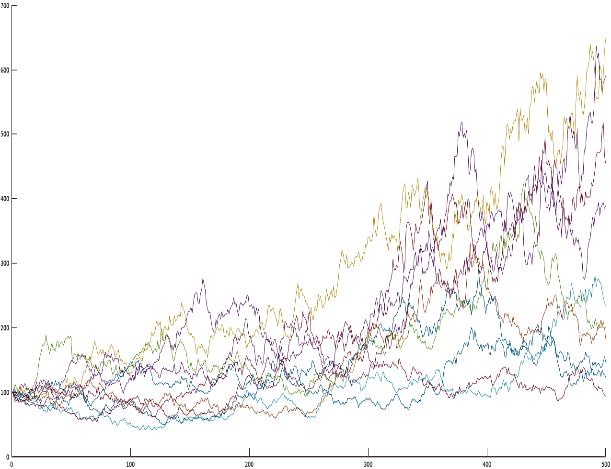Der Kurs Simulationsmethoden in der Finanzmathematik fokussierte sich hingegen auf den Aktienmarkt und dessen „Optionen“, allen voran der sogenannten Call Option. In erster Linie war das Ziel des Kurses, den fairen Preis einer Call Option zu bestimmen (fairer Preis = keine Arbitrage Möglichkeiten d.h. keine Möglichkeiten, ohne Eigenkapital risikolos Gewinn zu machen). Dafür wird die sogenannte „Quasi Montecarlo“ Methode angewandt. Mit dieser Technik werden Zufallsvariablen „konstruiert“ und bieten deswegen eine größere Verlässlichkeit, da Elemente der Wahrscheinlichkeitstheorie und geometrische Folgenanwendungen gemeinsam verwendet werden. Nachdem die Theorie größtenteils geklärt war, ging es nun mit dem Open Source Programm „Octave“ ans Programmieren. Nach reichlichen Matrizenrechnungen und Vektorberechnungen konnte sich das Ergebnis sehen lassen. Die Grafik zeigt 10 simulierte Aktienkursverläufe mit realistischen Parametern, aus denen man den Mittelwert nehmen und somit eine relativ gute Prognose für den Verlauf eines Kurses abgeben kann; natürlich wird diese genauer und genauer, je öfter man dem Programm befiehlt zu rechnen. Hat man nun also diesen Mittelwert, muss man ihn nur noch in eine verhältnisweise einfache Formel einsetzen und schon hat man nach nur fünf Minuten den fairen Preis für eine Call Option.
In dieser Woche drehte sich aber nicht alles um Mathematik – nun, vielleicht nicht in erster Linie. Die Teilnehmer bekamen jeden Tag Knobelaufgaben gestellt, wie zum Beispiel geometrische Extremwertaufgaben, die nicht nur Formelkenntnis, sondern auch ein Um-die-Ecke-Denken erfordern. An einem anderen Tag sollten wir alle möglichen Arten von Rechtecken, die sich auf einem karierten Block bilden lassen, herausfinden. Abgesehen vom Rechnen wurden auch Schätzaufgaben gestellt, abwegig wie das Produkt der Massen zweier Steine oder der prozentuelle Rückstand des Siebten beim Olympia-Biathlon auf den Sieger; oder ganz simpel wie die Blattanzahl eines Buches oder der mittlere Geburtstag aller Anwesenden. An einem Abend wurde noch unser Allgemeinwissen in einem Quiz geprüft, das wir in Teams bestritten, und an einem anderen Abend stellten wir uns einem Fünfkampf mit Disziplinen wie Sudoku oder 5er Tic-Tac-Toe.
Eines der erstaunlichsten Dinge an dieser Projektwoche bleibt jedoch, wie man nicht nur die Stereotypen von Mathematikern trifft, mit Harry-Potter-Brille, kariertem Pullunder und Notizblock unterm Arm – zumindest nicht ausschließlich – sondern ganz normale Leute. Diese ganz normalen Leute blühen jedoch auf, wenn sie über Mathematik reden, und ihr ganzes angestautes Wissen über ihr Interessensgebiet freigeben können, was ihnen im alltäglichen Umfeld verwehrt bleibt. Ein großes Dankeschön an unsere Schule, dass sie diese Möglichkeit für ihre Schüler bereithält.
